Multi-step equations demand several operations to isolate the variable, unlike simpler equations․ These are fundamental in algebra, building a strong foundation for advanced math concepts․

Understanding these equations is crucial for problem-solving in various fields, including science, engineering, and everyday financial calculations, offering practical applications․

What are Multi-Step Equations?

Multi-step equations are algebraic equations that require more than one mathematical operation to solve for the unknown variable․ Unlike single-step equations, these involve combining like terms, applying the distributive property, and utilizing inverse operations—addition, subtraction, multiplication, and division—in a specific sequence․

For instance, an equation like 6n ⎯ 2 = -3n + 7 necessitates adding 3n to both sides, then adding 2, and finally dividing by 9 to isolate ‘n’․ These equations often include parentheses or fractions, adding layers of complexity that demand a systematic approach to arrive at the correct solution․

Why are they Important?

Mastering multi-step equations is vital because they represent real-world scenarios far more accurately than simple equations․ They build critical thinking and problem-solving skills, essential across disciplines․ These skills translate to analyzing complex situations and formulating logical solutions․

Furthermore, they form the bedrock for advanced algebraic concepts, including systems of equations and inequalities․ Proficiency in solving these equations unlocks success in higher-level mathematics and prepares students for STEM fields, where analytical reasoning is paramount․

Understanding the Order of Operations

Order of operations, often remembered as PEMDAS/BODMAS, dictates the sequence for solving mathematical expressions, ensuring consistent and correct results every time․

PEMDAS/BODMAS Review

PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction) provides a standardized order for evaluating expressions․

This ensures everyone arrives at the same solution․ Parentheses/Brackets are addressed first, followed by exponents/orders․ Then, multiplication and division are performed from left to right, and finally, addition and subtraction, also from left to right․

Mastering this order is vital when simplifying equations before isolating the variable, preventing errors and guaranteeing accurate results․

Applying Order of Operations to Equations

When tackling multi-step equations, PEMDAS/BODMAS isn’t just for simplifying expressions; it dictates the sequence of operations to isolate the variable․ Begin by addressing any parentheses or brackets through distribution or simplification․

Next, combine like terms on each side of the equation․ Then, utilize inverse operations – addition/subtraction, multiplication/division – following the order of operations to move towards isolating the variable․

Consistent application prevents errors and ensures a correct solution․

Simplifying Equations Before Solving

Simplification streamlines the solving process․ Combining like terms and applying the distributive property reduces complexity, making it easier to isolate the variable effectively․

Combining Like Terms

Combining like terms involves merging similar variables raised to the same power․ For instance, in the equation 3x + 5x ⎯ 2 = 16, ‘3x’ and ‘5x’ are like terms․ Adding them results in 8x ⎯ 2 = 16․ This simplification reduces the equation’s complexity before isolating the variable․

Remember, you can only combine terms with the same variable and exponent․ Constants (numbers without variables) are also like terms and can be combined separately․ This step is crucial for efficient equation solving․

Distributive Property

The distributive property allows you to multiply a number by a sum or difference inside parentheses․ For example, 2(x + 3) becomes 2x + 6․ You multiply the 2 by both ‘x’ and ‘3’ individually․ This is essential when parentheses block direct combination of terms․

Applying this property removes the parentheses, transforming the equation into a simpler form ready for combining like terms and isolating the variable․ Mastering distribution is key to solving complex multi-step equations effectively․

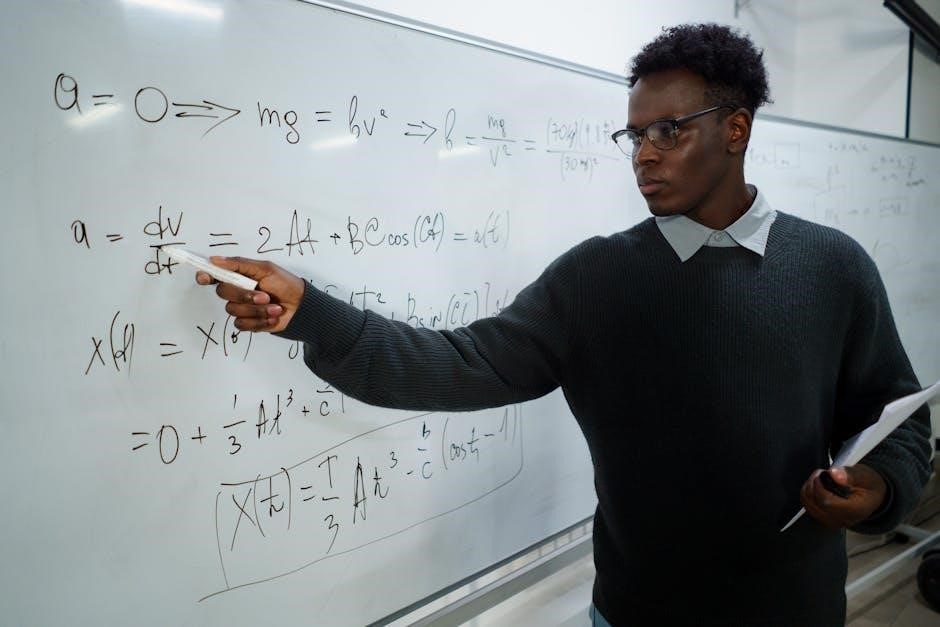
Isolating the Variable

Isolating the variable means performing inverse operations to get the unknown alone on one side of the equation, revealing its value․

Using Inverse Operations (Addition/Subtraction)

To isolate a variable, employ inverse operations․ If an equation includes adding a number, subtract it from both sides to maintain balance․ Conversely, if subtracting, add to both sides․

For instance, in the equation x + 5 = 12, subtract 5 from each side, resulting in x = 7․ Similarly, if x ‒ 3 = 8, adding 3 to both sides yields x = 11․

These operations effectively ‘undo’ the original operation, moving closer to isolating the variable and solving the equation․

Using Inverse Operations (Multiplication/Division)

When a variable is multiplied, utilize division to isolate it; conversely, if divided, multiply both sides of the equation․ Maintaining balance is paramount throughout the solving process․

Consider 7x = 21․ Dividing both sides by 7 gives x = 3․ If x/4 = 5, multiplying both sides by 4 results in x = 20․

These inverse operations effectively ‘undo’ the original operation, bringing you closer to finding the solution for the unknown variable․

Solving Equations with Fractions

Equations with fractions require finding a common denominator, often the Least Common Denominator (LCD), to eliminate fractions and simplify the equation for solving․

Finding the Least Common Denominator (LCD)

Determining the LCD is a vital step when tackling equations containing fractions․ The LCD represents the smallest number divisible by all denominators present in the equation․ For instance, if denominators are 2, 4, and 6, the LCD is 12․

To find it, list multiples of each denominator until a common multiple emerges․ Alternatively, prime factorization can be employed to identify the highest powers of all prime factors involved․ Multiplying these highest powers yields the LCD, enabling efficient fraction elimination․

Multiplying Each Term by the LCD

Once the LCD is established, the next crucial step involves multiplying every term within the equation by this value․ This strategic move effectively eliminates all fractions, transforming the equation into a more manageable form without fractional coefficients․

Ensure each term, including constants, receives this multiplication․ This process maintains equation balance while simplifying the structure, paving the way for straightforward variable isolation and ultimately, solution attainment․ Careful distribution is key!

Solving Equations with Parentheses

Parentheses introduce complexity, requiring the distributive property to expand expressions․ Simplifying inside the parentheses first is also a vital step for accurate solving․

Applying the Distributive Property

The distributive property is key when parentheses are present․ It involves multiplying the term outside the parentheses by each term inside․ For example, 3(x ⎯ 2) becomes 3x ‒ 6;

This step eliminates the parentheses, simplifying the equation․ Carefully apply the multiplication, paying attention to signs – a negative sign distributes as well! Failing to distribute correctly is a common error, leading to an incorrect solution․ Always double-check this step before proceeding․

Simplifying Inside the Parentheses First

Before distributing, always simplify expressions within the parentheses․ This means combining like terms or performing any addition or subtraction inside․ For instance, if you have 2(3x + x ⎯ 1), combine 3x and x to get 4x․

Then, the equation becomes 2(4x ⎯ 1)․ Simplifying inside first reduces complexity and minimizes errors during distribution․ Remember the order of operations – parentheses first, then distribution!

Checking Your Solution

Verification is key! Substitute your solved value back into the original equation to confirm it holds true, ensuring accuracy and solidifying your understanding․

Substitution Method

The substitution method involves replacing the variable in the original equation with the value you’ve calculated as the solution; For example, if you find ‘n’ equals 1, substitute ‘1’ for every ‘n’ within the equation․

This allows you to simplify both sides independently․ If, after substitution and simplification, the left side equals the right side, your solution is correct․ As demonstrated with 6n ‒ 2 = -3n + 7, substituting n=1 yields 4=4, confirming the solution’s validity․

Verifying the True Statement

Verification is a critical final step․ After substituting your solution back into the original equation, simplify both sides meticulously․ The goal is to determine if the resulting statement is demonstrably true․

If the left-hand side precisely matches the right-hand side – like achieving ‘4 equals 4’ – you’ve successfully solved the equation․ This confirms your answer’s accuracy and provides confidence in your algebraic manipulation skills, ensuring a correct result․

Example 1: Basic Multi-Step Equation

Let’s illustrate with 6n ⎯ 2 = -3n + 7․ Substituting n=1 yields 6(1) ‒ 2 = -3(1) + 7, simplifying to 4 = 4, confirming the solution․

Step-by-Step Solution

To solve 6n ⎯ 2 = -3n + 7, begin by adding 3n to both sides, resulting in 9n ‒ 2 = 7․ Next, add 2 to each side to isolate the term with ‘n’, yielding 9n = 9․ Finally, divide both sides by 9 to solve for ‘n’, obtaining n = 1․ This methodical approach ensures accuracy and clarity throughout the process․

Remember to perform inverse operations consistently on both sides of the equation to maintain balance and arrive at the correct solution․ Careful execution of each step is key!

Verification of the Solution

To verify n = 1 in the equation 6n ‒ 2 = -3n + 7, substitute 1 for ‘n’․ This yields 6(1) ‒ 2 = -3(1) + 7․ Simplifying, we get 6 ‒ 2 = -3 + 7, which further reduces to 4 = 4․ Since both sides of the equation are equal, the solution n = 1 is confirmed as correct․

This substitution method demonstrates the solution’s validity, ensuring a true statement results when the value is plugged back into the original equation․

Example 2: Equation with Distributive Property

Consider 3(x ⎯ 2) ‒ 5 = 4(2x + 1) + 5․ Applying the distributive property is key to simplifying and then solving for the variable ‘x’․

The distributive property is vital when parentheses exist within an equation․ It allows us to multiply a number by each term inside the parentheses; For instance, in 3(x ‒ 2), we multiply 3 by both ‘x’ and ‘-2’, resulting in 3x ⎯ 6․

This step eliminates the parentheses, simplifying the equation․ Remember to pay close attention to signs – a negative sign before parentheses changes the sign of each term inside․ Correct application is crucial for accurate equation solving, avoiding common errors and ensuring a correct final answer․

Solving for the Variable

Isolating the variable is the core of equation solving․ After simplification, use inverse operations to move terms around․ If a variable is multiplied, divide both sides; if added, subtract․

For example, if you have 7x = 7, dividing both sides by 7 yields x = 1․ Maintaining balance – performing the same operation on both sides – is paramount․ This methodical approach guarantees you arrive at the correct solution, revealing the variable’s value․

Example 3: Equation with Fractions

Fractional equations require finding the Least Common Denominator (LCD) to eliminate fractions․ Multiplying each term by the LCD simplifies the equation for solving․

Finding the LCD

Identifying the LCD is paramount when tackling equations containing fractions․ Begin by listing the denominators present in the equation – for instance, 2, 4, and 6․ Next, determine the smallest number divisible by each of these denominators without any remainders․

In our example, the LCD is 12, as 12 is divisible by 2, 4, and 6․ This LCD will be used to eliminate the fractions, transforming the equation into a more manageable form for solving․ Accurate LCD determination is key to success!

Solving After Multiplying by the LCD

Once each term in the equation is multiplied by the Least Common Denominator (LCD), the fractions disappear, leaving a standard linear equation․ Now, apply the principles of isolating the variable using inverse operations – addition, subtraction, multiplication, and division․

Simplify both sides of the equation, combining like terms as needed․ Continue these steps until the variable stands alone․ Finally, substitute the solution back into the original equation to verify its accuracy, ensuring a true statement․

Common Mistakes to Avoid

Common errors include incorrectly applying inverse operations and neglecting the distributive property, leading to inaccurate solutions․ Careful attention to detail is key!

Incorrectly Applying Inverse Operations

A frequent mistake arises when students misapply inverse operations․ For instance, adding instead of subtracting, or multiplying when division is required, disrupts the equation’s balance․ Remember, operations must be performed on both sides to maintain equality․

Carelessly changing signs or overlooking the order of operations can also lead to errors․ Always double-check each step, ensuring the inverse operation directly undoes the original operation, preserving the equation’s integrity and leading to the correct variable isolation․

Forgetting to Distribute

A common error involves neglecting the distributive property when parentheses are present․ Failing to multiply the term outside the parentheses by each term inside results in an unbalanced equation and an incorrect solution․ This oversight significantly alters the equation’s structure․

Always remember to carefully distribute before combining like terms or applying inverse operations․ Thoroughly checking this step prevents significant errors and ensures accurate simplification, ultimately leading to the correct answer․

Resources for Further Practice

Numerous online tools and downloadable worksheets are available to enhance your skills․ These resources provide ample practice and solidify your understanding of these equations․

Online Equation Solvers

Several websites offer online equation solvers that can assist in checking your work or providing step-by-step solutions․ These tools are incredibly helpful for verifying answers and understanding the process․ Websites like Symbolab and Mathway can solve multi-step equations, displaying each operation performed․

However, remember that relying solely on solvers hinders skill development․ Use them as a learning aid, not a replacement for practicing problem-solving independently․ Understanding the ‘why’ behind each step is paramount for true mastery․

Worksheet PDFs

Numerous websites provide free, downloadable worksheet PDFs focusing on multi-step equations․ These resources offer targeted practice, allowing students to hone their skills independently․ Khan Academy and Math-Drills are excellent sources, providing varying difficulty levels․

Working through these worksheets reinforces concepts and builds confidence․ Printing and completing them manually encourages a deeper understanding than solely digital practice․ Consistent practice with diverse problems is key to mastering multi-step equation solving․

Advanced Multi-Step Equations

These equations involve variables on both sides and multiple parentheses, requiring skillful application of distribution and inverse operations for accurate solutions․

Equations with Variables on Both Sides

When variables appear on both sides of the equation, the primary strategy involves manipulating the equation to consolidate these variable terms․ This is typically achieved by applying inverse operations – addition or subtraction – to move one variable term to the opposite side․

Subsequently, proceed with simplifying both sides by combining like terms and then isolating the remaining variable using multiplication or division․ Remember to perform the same operation on both sides to maintain equation balance, ensuring an accurate solution․ Careful attention to signs is paramount throughout this process․

Equations with Multiple Parentheses

Equations featuring multiple sets of parentheses necessitate a systematic approach․ Begin by meticulously applying the distributive property to each set of parentheses, expanding the equation․ This step eliminates the parentheses and transforms the equation into a more manageable form․

Following distribution, combine like terms on each side of the equation․ Then, proceed to isolate the variable using inverse operations, mirroring the techniques employed in simpler multi-step equations․ Accuracy in distribution is key to avoiding errors․

Real-World Applications

Multi-step equations model countless real-world scenarios, from calculating distances and costs to determining mixtures and investments, offering practical problem-solving skills․

Word problems translate these situations into algebraic expressions, requiring careful setup and solution using the learned techniques․

Word Problems Involving Multi-Step Equations

Translating real-world scenarios into mathematical equations is a key skill․ These problems often require identifying unknown quantities and representing them with variables․

For instance, consider a problem involving total costs: “A plumber charges a $50 service fee plus $75 per hour․ If the total bill is $350, how many hours did the plumber work?”

This translates to 50 + 75h = 350․ Solving for ‘h’ requires multiple steps – subtraction, then division․ Practice with diverse word problems builds proficiency in equation formulation and solution․

Using Equations to Model Scenarios

Mathematical modeling involves representing real-life situations with equations․ This allows us to analyze and predict outcomes based on given conditions and relationships․

Imagine modeling a savings plan: “You start with $200 and save $30 each week․ How many weeks will it take to save $500?” This becomes 200 + 30w = 500․

Successfully modeling requires careful identification of variables, constants, and the relationships between them․ This skill is invaluable in fields like physics, economics, and computer science․